Je bosse sur de la photo, des images, et je vais vous montrer pourquoi les maths c’est vraiment sympa quand on se penche un peu sur la question. Et c’est “tous niveaux”, ou presque. Allez, disons niveau lycée.

Vous ne connaissez peut-être pas le nom de l’effet “Bleach Bypass” (passage à l’eau de javel dans la langue de Jean-Claude Van Damme), mais vous avez sûrement déjà vu des images traitées avec cet effet. C’est un effet qui donne une impression “délavée”, très dramatique, brûlée. Steven Speilberg l’a utilisé dans “Il faut sauver le soldat Ryan”, mais on le retrouve dans plein d’autres oeuvres cinématographiques. Par exemple “300” de Zack Snyder, ou encore dans “Seven” de David Fincher.

Et les photographes se sont aussi emparé de cet effet.

Vous avez le droit de ne pas aimer cet effet, mais ce n’est pas le sujet de l’article.

Cet effet, expliqué sur la page Wikipedia, est assez simple à mettre en place dans la plupart des logiciels. Sans math, juste avec quelques paramètres et un peu de flair.

(By Soerfm - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=29205537)

L’effet est simple, sur Blender par exemple

J’adore Blender. C’est un superbe outil pour faire des images de synthèse, du montage vidéo, des animations, et plein d’autres trucs. Je l’utilise depuis 1999, c’est dingue ce qu’il a évolué.

Et il a aussi un outil de “compositing”, en d’autres termes, on peut manipuler des vidéos et des photos pour faire du montage et du travail de “post production”.

Et je peux faire ce genre d’effet dans le “compositeur” d’image. C’est pas très compliqué :

• désaturer l’image (lui enlever de la couleur)
• passer par une courbe pour écraser les ombres et forcer les lumières
• et faire un “overlay” (une surcouche) de ce résultat sur l’image originale

Et ça marche plutôt bien.

L’image de référence, elle vient de cet article de Tristan Kneschke, que je vous recommande fortement : https://www.premiumbeat.com/blog/color-grading-bleach-bypass-look-in-davinci-resolve/. Le résultat m’a permis de comparer mes opérations à ce qu’il propose, et franchement ça m’a énormément aidé.

Dans Blender, clairement, il y a assez d’outils pour faire ça vite. Mais y’a pas que Blender dans la vie…

ComfyUI, un outil pour faire des images avec l’IA

Et puis je me dis que ce serait cool de faire ce “nœud” de traitement dans ComfyUI, c’est un outil qui permet de créer des images avec des modèles (de l’IA en veux-tu), et qui permet de faire des “flux” (workflow).

Sauf que ComfyUI n’a pas de nœud pour manipuler une courbe. Cela ne veut pas dire qu’on ne peut pas le faire, mais il va falloir changer de méthode. Le plus simple, pour moi, développeur, c’est de créer mon propre nœud en Python.

Mais, si je ne peux pas faire un éditeur de courbe comme sur Blender, quel outil me reste-t-il ?

La réponse…

Les maths !

Holla, avant de lire la suite

L’idée de cet article, ce n’est pas de faire le kéké en math. Ce que je vais vous montrer, n’importe quel mathématicien ou bon matheux vous dira que c’est “super simple”.

Moi, je suis conscient que ce n’est pas évident pour tout le monde.

Mon but, là, ce n’est pas de vous faire peur ou de vous faire sentir comme étant idiot parce que ce que vous ne comprenez pas le principe que je vais montrer. C’est tout l’inverse !

En fait, je vais vous demander, en lisant ces lignes, de partir du principe que ça va être assez simple.

Vous allez voir que je ne cherche pas à expliquer des trucs difficiles en math, mais au contraire de passer outre des concepts et ne s’intéresser qu’à ce qui va nous servir.

C’est exactement le but. Vous allez voir qu’on va se foutre royalement de ce que fait telle fonction ou telle opération. On va juste se servir des outils et y aller à l’arrache.

Et donc, au final, je vous dirai un truc sur les math en conclusion qui va vous “étonner”… mais lisez d’abord le boxon qui suit 😄

La courbe en “S”

Ce que j’essaie de faire, c’est d’arriver à reproduire un minimum de choses que je fais avec des machins à la souris, mais en calcul pur. Alors, autant la formule pour la partie de traitement appelée “overlay” est chiante à mourir, autant la courbe en “S” est assez sympa à manipuler.

Si si, je vous assure que c’est sympa, mais il va falloir accepter un truc : ne pas avoir peur des symboles mathématiques, des noms de fonction ou encore de l’écriture.

Les courbes en “S”, il en existe des tas qui sont définies en math. On les appelle comme ça parce que leur forme ressemble à un “S”.

Sans être un gros matheux, si votre mémoire est bonne (mais je vais vous la rafraichir), il existe une courbe qu’on a déjà vue au lycée qui a cette forme de “S”. La fonction “tangente hyperbolique”.

$$tanh(x)$$

Alors, on va être clair, on se fout de savoir d’où elle vient, ce qu’elle fait dans la vie, le nom de son chat etc. Ce qui nous intéresse, c’est la forme qu’elle a.

Voilà, ça ressemble à un “S” et c’est ce qu’on veut.

Et là j’insiste, c’est ce qu’on veut, POINT. On sait que cette fonction a, à peu près, la forme qu’on veut, et c’est tout ce dont on a besoin pour le moment.

Dans Blender, on dessinait cette courbe à la main, avouez que ça ressemble à la fonction mathématique \(tanh\) :

Bon par contre y’a un ou deux trucx qui ne vont pas…

• De manière pragmatique, la courbe dans Blender, elle part de 0 et elle va vers 1, alors que la tangente hyperbolique, elle pond aussi des valeurs négatives et elle s’étire pratiquement vers “2”. Ça, c’est pas cool pour nous.
• Et puis, dans Blender, je peux vraiment bouger la courbe comme je veux, la rendre plus plate, plus tendue, forcer les valeurs hautes, etc. alors que là, bah j’ai juste une fonction qui fait un “S”.

En gros, je veux ça, dans le carré vert, on se fiche de ce qui dépasse :

Vous devez bien capter ce que vous voyez : là, la courbe, elle passe par \(0,0\) et \(1,1\), c’est à dire les coins du carré vert. C’est hyper important, il faut que la courbe passe par ces deux points. sinon, on va perdre plein de pixels de notre image quand on va la traiter.

Sploier alert : on va y arriver.

C’est à ce moment qu’il faut prendre son courage à deux mains, et se dire que bon, OK c’est pas complètement bon, mais on doit pouvoir “modifier” cette fonction \(tanh(x)\) pour qu’elle colle au besoin.

La formule magique (c’est pas “s’il te plait”", c’est des maths)

Alors, il faut soit se souvenir des cours de maths du lycée, soit aller poser la question à des gens, des IA, potes, ce que vous voulez.

Mais je vous donne la réponse, elle se résume en cette formule :

$$k*(x-b)+c$$

En fait, dans cette formule qui semble barbare, seules \(x\) est variable, c’est la valeur d’un pixel, la note des élèves, un niveau sonore, votre salaire mensuel dans votre tableau Excel…

Les trois autres, c’est nous qui choisissons les valeurs, au besoin, selon la situation.

Il faut se souvenir que :

• \(k\) change la pente d’une courbe
• \(b\) déplace la courbe à droite et à gauche (on appelle ça un “offset horizontal)”
• \(c\) déplace la courbe de haut en bas (on appelle ça un “offset vertical”)

C’est le truc le plus compliqué de l’article… vous notez cette formule quelque part, vous le gardez, c’est vraiment un truc à retenir. Je m’en sers plus souvent que vous ne pouvez le croire, pour travailler sur un tableur (pas Excel), quand je dois analyser des données, en imagerie, partout je vous dis.

On n’a pas besoin de bouger la courbe verticalement, donc on va virer \(c\) de notre formule pour le reste de l’article.

Et ça marche avec n’importe quoi. Ces règles, bien appliquées, vous pouvez les utiliser sur toutes les fonctions qui prennent “x” en entrée. Vous choisissez des valeurs “k” et “b” (appelez les comme vous le voulez hein), et ça fonctionne.

La preuve en image interactive (réglez k et b pour voir):

Par contre, faut pas se planter, je dois bien multiplier l’ensemble “\(x+b\)” par “\(k\)”, les parenthèses sont importantes :

$$k*(x+b)$$

Mais vraiment, au pire, gardez juste la règle “\(k(x+b)\)” en tête et appliquez là au besoin. Par exemple, si je vous propose une fonction \(P_{rout}(x)\) qui fait un superbe prout mathématique, vous pourrez la transformer en \(P_{rout}(k(x+b))\), et donc l’écraser et la décaler sous le nez du voisin.

On applique

Donc, je prends \(tanh(x)\) et je lui ajoute mes valeurs \(k\) et \(b\) pour faire les transformations que je veux :

$$S(x) = tanh(k.(x+b))$$

C’est tout… J’ai pas tortillé 2 ans, j’ai juste appliqué la formule magique.

Avec \(k\) et \(b\) des valeurs que je vais choisir pour avoir la forme que je veux. \(k\) modifie la pente, et \(b\) le décalage à droite et à gauche.

Je sais, donc, changer la “force” de la courbe (sa pente), et je sais la déplacer… mais dans le mauvais sens crénondedjiou.

Et oui, si \(b\) vaut, par exemple, \(0,5\) alors la courbe se déplace à gauche. Grrrrrr. Pas content.

On va donc soustraire au lieu d’additionner, ce sera plus naturel :

$$S(x) = tanh(k.(x-b))$$

Voilà !

Bon, en animant \(k\) et \(b\) (merci à Desmos, ce site est génial), on peut voir comment agissent les valeurs sur la courbe (la droite en bleu c’est une représentation de la pente qui est modifiée par “k”, et le point “b” c’est pour vous indiquer le décalage) :

Posez vous deux secondes, je vous résume ça.

On n’a pas fait un truc de fou, je vous assure. Au pire acceptez simplement le principe :

• j’ai pris une fonction qui a la tête d’un “S” parce que c’est ce que je veux
• j’ai fait en sorte de pouvoir faire glisser la courbe à gauche ou à droite en ajoutant une valeur “b”
• j’ai fait en sorte de pouvoir l’écraser, simplement en multipliant la valeur “x” par une valeur que j’appelle “k”
• c’est assez simple : on multiplie pour accélérer, on ajoute pour avoir de l’élan

Clairement, on est pas mal là. Sauf qu’on voit un petit souci. Oh, rien de bien méchant…

Là, on a juste trouvé comment changer la pente et la position de la courbe. Mais on est toujours pas dans le carré vert, c’est-à-dire qu’on ne sait pas encore utiliser seulement des valeurs entre 0 et 1, et retourner des valeurs qui doivent passer par 0 et 1 en y.

Ce que je vous dis, clairement, c’est que la courbe en \(x=1\) ne donne pas 1. Et en 0, on a des valeurs négatives (la courbe passe à gauche, et est en dessous de 0) alors qu’on doit retourner 0.

Il va falloir utiliser une opération connue en informatique : la normalisation

Normalisation de la courbe

Une normalisation, c’est une opération qui vise à transformer des valeurs dans un intervalle donné entre deux autres valeurs choisies.

En français, notre fonction balance des valeurs entre -1 et 1, on veut qu’elle se place entre 0 et 1.

Sachant que nous allons lui envoyer, en entrée, que des valeurs entre 0 et 1, parce qu’une image ça marche comme ça et puis c’est tout, on n’a pas à s’occuper de ce qui est en dehors de cet intervalle.

Alors, je ne vais pas passer par 42 chemins, une normalisation ça se calcule comme ça :

$$\frac{x - m_{inimum}}{m_{aximum}-m_{inimum}}$$

Et nous, comme on tape entre 0 et 1, on va prendre les valeurs \(S(0)\) et \(S(1)\) pour le minimum et le maximum.

Donc, prenez votre respiration :

$$\frac{S(x) - S(0)}{S(1) - S(0)}$$

Et ça, c’est notre courbe en S pour changer la lumière et les ombres d’une image. On pourra paramétrer la force avec \(k\) et corriger la dose d’ombres et de lumière avec \(b\).

Voilà, on y est. En modifiant \(k\) et \(b\) on arrive à avoir à peu près tous les types de réglages que l’on veut pour faire adapter l’image et passer à la suite.

Je veux juste qu’on soit bien clairs entre nous. La fonction qu’on a créée, elle a deux valeurs qui nous servent de réglage. \(k\) et \(b\). Alors que \(x\) sera la valeur de chaque pixel de l’image, en réalité chaque couleur de chaque pixel de l’image. De mon côté, j’utilise cette fonction en Python, mais en vérité, vous pouvez la “coder” avec Blender (avec les nœuds), l’utiliser dans Excel ou OnlyOffice, avec autre chose que \(tanh\).

Le “overlay”

Ce sera moins compliqué, on va juste appliquer la formule pour faire ce qu’on appelle un “Overlay”. En gros, ce que fait cette opération, surtout utilisée pour le traitement d’image, c’est de prendre deux images : une “base” et une “couche supérieure”. Là où la base est sombre, la couche supérieure doit devenir plus sombre, et là où la base est claire, la couche supérieure doit l’être encore plus.

C’est une opération qui vise, donc, à utiliser une image comme référence d’ombres et lumières pour régler la seconde (la sortie).

La formule est décrite dans la page Wikipedia https://en.wikipedia.org/wiki/Blend_modes#Overlay et elle utilise une condition.

On prend \(a\) et \(b\), avec \(a\) étant la base, et \(b\) la couche supérieure.

• Si \(a\) est inférieur à 0,5, alors on fait “\(2 *a* b\)”",
• sinon on doit faire \(1-2(1-a)(1-b)\)

En écriture plus “matheuse” on écrit :

$$ \begin{align} O_{verlay}(a,b) = \left\{ \begin{array}{cl} 2ab & \text{si } a < 0,5 \\ 1-2(1-a)(1-b) & \text{si } a\ge0,5 \end{array} \right. \end{align} $$

Il faut juste savoir une chose ici, \(a\) et \(b\), ce sont les valeurs qu’on va prendre dans la tronche, les couleurs de chaque pixel, les une après les autres. Mais en Python, avec numpy, on ne se prend pas la tête. On code les opérations comme si c’était une seule valeur, alors qu’en réalité, on reçoit l’image en entier (un tableau, de valeurs à plein de dimensions) - c’est lui qui se débrouille. On est de sacrés fainéants, mais c’est pour ça qu’on aime Python.

Ce ne sont que des multiplications, des additions et des soustractions. Je vous assure, prenez le temps de lire, c’est relativement simple..

On passe à Python

Je ne vous donne pas le code complet du “nœud” de ComfyUI que je développe, parce qu’il y a tout un pan de qui sert à la présentation dans l’interface, la gestion des entrées etc.

Avant de lire, sachez que je vais utiliser numpy, puisqu’il simplifie grandement les algorithmes à développer. En gros, au lieu de faire le calcul moi-même, pixel par pixel, couleur par couleur, il va le faire pour moi… Numpy gère les matrices sans qu’on ait à se battre avec les boucles.

La fonction de base, c’est le calcul \(tanh(k.(x-b))\) :

import numpy as np

def T(x:np.ndarray, k: float, b: float) -> np.ndarray:
  return np.tanh(k*(x-b))

# en mode dégueux on ne donnerait pas les "tupes" attendus
def T(x, k, b):
  return np.tanh(k*(x-b))

# ça marche aussi, mais c'est infâme à utiliser dans les éditeurs de code... pensez à
# indiquer les types attendus, ça aide grandement

“x”, ici, c’est l’image sous formel de tableau de valeurs. Quand je vous dis que c’est simple avec numpy…

Alors, oui, je me balade les valeurs “k” et “b” partout, parce que je ne veux pas les mettre en “valeur globale”. C’est une habitude quand on développe, mais sachez que vous auriez pu faire :

# avant de créer la fonction
k=3
b=0.5

# et en gros:
def T(x):
  return np.tanh(k*(x-b))

# c'est simple à lire, mais encore une fois c'est pas pro ça

Bon, pour la normalisation, on a plein de manière de faire, mais le calcul “manuel” est plus clair :

def Tnorm(x:np.ndarray, k:float = 3.5, b:float = .5) -> np.ndarray:
  return ( T(x, k, b) - T(0, k, b) ) / (T(1, k, b) - T(0, k, b))

On a notre effet… ou presque.

Alors, encore une fois, je vous passe les détails, mais en fait, il va manquer deux trois trucs pour que ça marche.

• il faut savoir ouvrir une image, notamment en utilisant le package PIL (Pillow)
• en réalité, on doit désaturer (réduire les couleurs, en gros) l’image avant de la passer dans la courbe en “S”
• on doit avoir un facteur pour régler à quel point on prend l’une ou l’autre image dans le “overlay”

Bref, pour vous aider à comprendre, j’ai créé un notebook, cliquez sur ce bouton pour voir le code et le résultat :

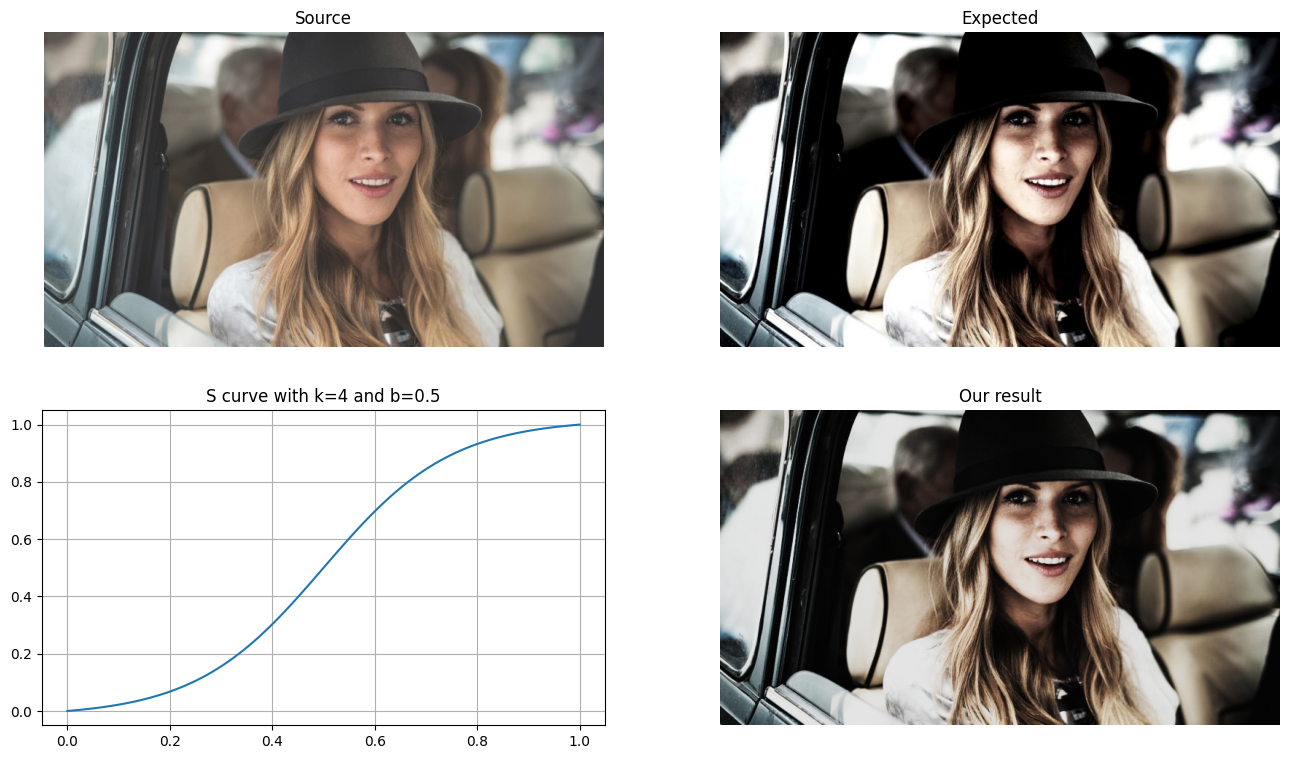
Et le résultat final comparé à l’article de référence que j’ai utilisé :

Merci à Tristan Kneschke pour son excellent article traitant de cet effet photo pour le logiciel “DaVinci Resolve”. Son travail m’a servi de référence pour Blender et pour le code que j’ai produit.

Son article est ici : https://www.premiumbeat.com/blog/color-grading-bleach-bypass-look-in-davinci-resolve/

Et donc, avec ComfyUI ?

Et bien j’ai créé un nœud qui utilise le code que je vous présente dans le notebook. Y’a pas mal de code pour la gestion des “tenseurs” (et oui, faut pas déconner non plus, tout n’est pas si simple). Mais il marche pas mal du tout !

Le projet est en cours de “push”, sur ma page github - patience… je dois nettoyer le code, documenter, tout ça…

Ce n’est pas grand-chose, mais ça le fait.

Et ça marche, évidemment, avec les images générée par l’IA…

Le truc étonnant, c’est cette récupération d’ombre en fond d’image, invisible dans l’image générée. Cet effet est très étonnant.

Les maths, c’est cool, vraiment

Il se peut que vous n’ayez vraiment pas capté ce que j’ai raconté. J’en suis désolé et non ça ne fait pas de vous un idiot ou une personne en dessous des autres. Certaines personnes calent sur les maths, d’autres, c’est sur la psychologie, et d’autres sur la mécanique.

Ce que j’ai tenté de vous montrer, c’est qu’il n’est pas nécessaire d’avoir un bagage de malade pour faire des trucs en math. Croyez-le ou non, je n’ai utilisé ici que des multiplications et des additions. Inutile de comprendre ce qu’est une tangente hyperbolique, ou de savoir pourquoi la formule de normalisation est comme ça. Si vous avez juste une idée de la forme d’une fonction, ou de ce qu’elle peut donner comme résultat, alors vous pouvez les utiliser comme des outils.

Je ne sais pas comment fonctionne mon réseau de flotte dans la maison, pourtant je sais me servir d’un robinet. Et bah en math, on peut faire pareil. On peut utiliser une fonction sinus ou une normalisation pour sortir un résultat sans pour autant avoir toute la théorie qui mène à leur création.

Dans mon métier, je dois manipuler des fonctions Sigmoïde, tanh, des normalisations bizarres et des vecteurs à 1000 dimensions. Je vous assure que, dans le quotidien, je ne les utilise que pour sortir des résultats, je ne les étudie pas et je ne pourrais d’ailleurs pas toutes les expliquer. Je sais à quoi ça sert et comment les manipuler.

Il ne faut, au final, que deux choses : observer et trouver une astuce. C’est ce qu’on a fait dans cet article.

Cela ne m’a pas empêché, finalement, de me replonger dans la théorie par la suite, mais je vous assure que ce n’est pas une obligation.

Pour finir, il est évident que cet article s’adresse à ceux qui, potentiellement, ont envie d’apprendre à développer en Python des outils pour traiter le son et l’image, ou pour les gens qui utilisent des outils qui permettent de faire des opérations pour traiter des images (Blender, DaVinci Resolve, Gimp, Photoshop, etc.). Dans les faits, bien souvent, l’outil vous propose un bouton pour réaliser l’effet. Mais si vous voulez aller plus loin, voire créer votre propre effet à vous, et bah taper dans les maths, ce n’est pas déconnant.